Ren matematikk
Jo, i motsetning til anvendt matematikk, er det matematikk der hverken doktorgradsstudent, veileder eller forskningsformidler klarer å komme på en eneste anvendelse eller forenklet beskrivelse av forskningen, annet enn at det danner grunnlaget for mer ren matematikk….
Dette var den litt humoristiske opptakten når innholdet i doktorgradsavhandlingen til Jan Roksvold skulle forklares.
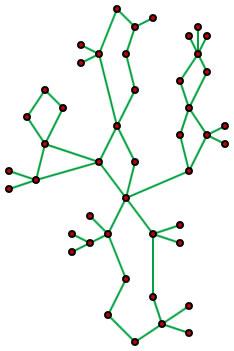 |
| Dette er en kaktusgraf som eksemplifiserer noe av det Roksvold har jobbet med, nemlig å beregne antallet kanter i løkkene i grafen. Illustrasjon: Wikipedia |
– Det er grunnforskning vi driver med, å fremskaffe mer kunnskap.
Vårt arbeid kan ikke umiddelbart knyttes opp mot folk sin hverdag men vi kan jo gjøre et forsøk på å tenke oss praktisk anvendelse, smiler Roksvold.
Feilretting i digitale meldinger
Matematikeren har jobbet med algebra og kombinatorikk* og forklarer at tilsvarende beregninger kan bedømme hvor god en «feilopprettende kode» er. For å forklare hva en feilopprettende kode er, kan man tenke seg et datasett som skal sendes fra en satellitt til en bakkestasjon på jorda. Når informasjonen sendes fra satellitten til bakkestasjonen vil det påløpe små feil i meldingen. En feilopprettende kode vil kunne justere og korrigere disse feilene umiddelbart, slik at meldingen som kommer frem til bakkestasjonen ligner den som ble sendt fra satellitten.
Den feilopprettende koden kan være god eller dårlig, dvs at den kan være finmasket og ta alle feil eller den kan være grovmasket og ta bare de groveste feilene.
En finmasket kode tar mye datakapasitet, mens en grovmasket kode gjør at sendingen går raskere og krever mindre kapasitet. Det er derfor hele tiden en vurdering som må gjøres der sikkerhet i meldingen måles opp mot tidsbruk og datakapasitet.
– Beregninger tilsvarende de jeg har jobbet med, kan si noe om hvorvidt den feilopprettende koden er bra eller dårlig. Deler av avhandlinga kan således sees som et bidrag til den brobygginga som gjøres mellom ren matematikk og kodeteori, forklarer han.
 |
| Jan Roksvold forsvarte sin doktorgradsavhandling i matematikk 8. september 2015. |
Kunnskap er målet – og kommer til anvendelse på sikt
Roksvold påpeker at grunnforskning er viktig selv om man i det øyeblikket forskningen utføres ikke har en klar formening om hva det kan brukes til annet enn å generere mer kunnskap. Mye grunnforskning ligger likevel til grunn for det som mange år senere blir anvendt.
Det ligger mye matematisk grunnforskning i bunnen av de prosesser som kjøres kontinuerlig i en vanlig mobiltelefon. Også banktjenester er basert på forskning som for 20 år siden var regnet som grunnforskning uten et klart mål om å «være nyttig».
Roksvold utførte sine beregninger ved hjelp av dataprogrammet Magma Computational Algebra System.
– Dette programmet er mye brukt til beregninger i algebra, tallteori og algebraisk geometri og har vært brukt til å bekrefte eller avkrefte våre hypoteser, avslutter han.
Tittel på doktorgradsoppgaven er: “Some combinatorial invariants determined by Betti numbers of Stanley-Reisner ideals”. Veiledere under arbeidet hans var Hugues Verdure og Trygve Johnsen ved Institutt for matematikk og statistikk.
*Kombinatorikk: Et område innen matematikken som går ut på å telle kombinasjoner av objekter i mengder som deles etter gitte regler og er nært beslektet med sannsynlighetsteorien. Man trenger en metode å finne antall mulige utfall, og antall måter et bestemt utfall kan opptre, for å beregne sannsynligheten for det nevnte utfallet. (Wikipedia)